Los problemas de dinámica de fluidos a menudo generan una lámina libre en geometría compleja y en muchos casos son altamente transitorios. Ejemplos en hidráulica son flujos sobre vertederos, en ríos, alrededor de pilares de puentes, inundaciones, flujo en válvulas y en otras muchas estructuras. Se puede resolver este tipo de flujos de una forma precisa y con recursos razonables de cálculo. Para ser útiles, las simulaciones deberían ir más rápido y ser más baratas que el empleo de modelos físicos.
Muchos programas de cálculo pueden resolver las ecuaciones en diferencias parciales que describen la dinámica de los fluidos. No muchos programas son capaces de incluir en estas ecuaciones el cálculo de la lámina libre. La dificultad es matemática que normalmente se refiere como el problema de la condición de contorno libre. Una condición de contorno libre tiene la dificultad de que por un lado, la región de cálculo cambia cuando su superficie se mueve, y por otro lado,el movimiento de la lámina libre es a cambio determinado por la solución.
Los cambios en la región de cálculo incluyen no sólo cambiar el tamaño y la forma sino que en algunos casos también pueden incluir regiones de incoalescencia y de rotura (ejemplo, la pérdida y ganancia de lámina libre)
En este artículo se habla sobre la técnica de modelado computacional con lámina libre. Esta técnica está basada en el método VOF (Colum – Of – Fluid). Esta técnica tiene propiedades únicas que la hacen especialmente aplicable a flujos en lámina libre. El objetivo es mostrar por qué la aproximación VOF ofrece una forma natural de capturar las superficies libres y su evolución con gran eficiencia.
Una buena recomendación para el método VOF es la de demostrar las capacidades en un simple problema de hidráulica que está alejado de ser trivial. El ejemplo seleccionado es de un flujo sobre un salto. Este flujo tiene una simplicidad conceptual y datos experimentales disponibles para validación (ver N. Rajaratnam and M.R. Chamani, “Energy Loss at Drops,” J. Hydraulic Res. Vol. 33, p.373, 1995).
.
Prototipo de flujo hidráulico con lámina libre
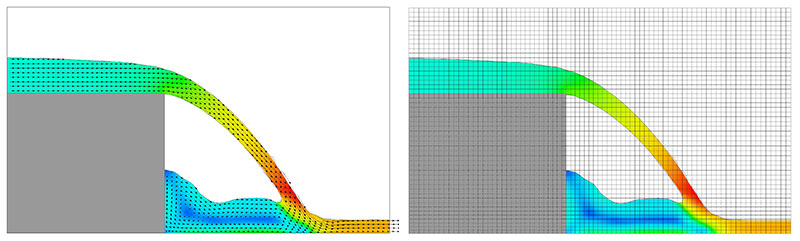
La Figura 1a muestra el problema del flujo después de que se haya alcanzado una condición de estado estacionario. El flujo del salto, tiene tanto una superficie libre aguas arriba y abajo. En la parte inferior de la desbordamiento se forma una balsa entre el labio y la pared del escalón, mientras que aguas abajo, el líquido está fluyendo hacia la derecha con una superficie plana y estable. Estrictamente hablando, las condiciones de flujo en la región de la balsa no son estables debido a la mezcla turbulenta que se genera en la balsa por el fluido que incide. Hay, sin embargo, una configuración media y que es lo que se reportó en los experimentos.
De forma práctica, el flujo es de dos dimensiones, es decir, que no tiene ninguna variación significativa en la dirección normal a la ilustración en la Fig. 1a. De hecho, para tener un espacio de aire encima de la balsa debe haber alguna abertura a la atmósfera de lo contrario colapsaría.
La velocidad de flujo en la parte superior del salto es crítica, es decir, que tiene una velocidad igual o mayor que la velocidad de las ondas de superficie, de modo que no se producen perturbaciones de aguas abajo que puedan penetrar a través de esta región para afectar al flujo de aguas arriba (a la izquierda del salto), por lo que el flujo es excepcionalmente suave y constante en esa región.
Hay muchas características geométricas en este problema que se puede comparar con una simulación numérica; tales como alturas de flujo antes y después del salto, el ángulo de la corriente de rebosamiento cuando golpea la parte inferior y la profundidad de la balsa formada bajo el desbordamiento. Además, una comparación importante para las aplicaciones prácticas es la cantidad de energía (es decir, cinética más potencial) perdida por el flujo al pasar por encima del salto.
.
Simulación del Problema Prototipo
La Figura 1a proviene de una simulación CFD. Para este ejemplo todas las geometría y propiedades del material usados en el experimento se usaron en la simulación CFD.
La altura del salto usada en el laboratorio es de 62cm y el fluido es agua ordinaria (densidad 1.0 gm/cc y viscosidad dinámica=0.01dynes/cm). La profundidad del agua entrando en la región de cálculo wea 15.5cm y fue dada por una velocidad cercana a la crítica de 123.0cm/s. Por supuesto, la gravedad es en la dirección vertical con una magnitud de g=-980cm/s2.
Dado que se esperaba turbulencia en la balsa a la izquierda del flujo, se usó un modelo de turbulencia (RNG). Se realizaron posteriores simulaciones sin modelo de turbulencia con resultados muy similares, lo cual no es sorprendente dado que la mayor parte de los elementos importantes del flujo son suaves (no turbulencia), caudales de entrada, salto y salida.
La región de simulación que se muestra en la Fig. 1b tiene 170 cm de ancho y 100 cm de alto y se ha subdividido en un bloque de malla con celdas rectangulares de igual tamaño y que consta de 80 celdas en la dirección horizontal y 60 celdas en la dirección vertical, para un total de 4800 celdas. La malla se usa como base para las aproximaciones en diferencias finitas de las ecuaciones diferenciales que gobiernan la dinámica de fluidos (las ecuaciones de Navier-Stokes).
El número y el tamaño de las celdas de la malla se eligen con el objetivo de captar las estructuras más pequeñas del flujo que se pueden esperar según el problema. El número se puede aumentar o disminuir fácilmente si los resultados parecen justificar algún ajuste. De hecho, a menudo es una buena idea repetir una simulación con un cambio de tamaño de las celdas para asegurarse de que la solución no sea demasiado sensible a tales cambios.
Una condición contorno de tipo velocidad con altura específica de fluido fue elegida para la condición de contorno a la izquierda. La condición de contorno a la derecha fue fijada de tipo salida donde todas las cantidades del flujo tienen un gradiente normal nulo a este límite para fomentar un flujo de salida uniforme. Los límites superior e inferior son paredes rígidas, mientras que, en la tercera dirección, los límites se trataron como planos de simetría (es decir, paredes con arrastre nulo al fluido). La superficie del escalón también se trató como una condición de contorno con deslizamiento libre.
Las condiciones iniciales podrían haberse establecido para aproximarse a la disposición del flujo esperado, pero teniendo en cuenta que la configuración del flujo es una de las cosas que se quiere calcular, especialmente en situaciones en las que no se sabe cuál podría ser la distribución de fluido, un enfoque más simple es necesario.
Debido a que se realizó una simulación en régimen transitorio para este ejemplo, se definió una condición inicial simple que consistía en solo un bloque de fluido en la parte superior del escalón, la Fig. 1a con la misma velocidad horizontal y altura asignada en la condición de contorno de la izquierda. La simulación siguió hasta el desarrollo de un flujo constante, que se produjo después de unos 8,0 s. La simulación se extendió a un tiempo de 10.0s para asegurar que se hubieran alcanzado condiciones estables. La figura 2 muestra dos tiempos intermedios; 2.b a 0.2s y 2.c a 0.5s además del instante final en 2.d a 10.0s.
Se debe tener en cuenta que lo que comienza como una sola superficie libre conectada se transforma en dos superficies libres independientes (superficies superior e inferior) después de que el fluido golpea el fondo. No se experimentan dificultades con esta separación del flujo en porciones que fluyen a la izquierda y derecha del punto de impacto en el límite inferior. Esto se discutirá con mayor detalle en la siguiente sección.
En la siguiente tabla, podemos observar las comparaciones (con gran concordancia) entre el experimento y la simulación:
| Tabla comparativa | Resultados experimentales | Resultados de la simulación |
| Altura de salida / altura del escalón | 0.094 | 0.094 |
| Altura de la piscina / Altura del escalón | 0.41 | 0.41 |
| Ángulo de impacto en el límite inferior | 57° | 59° |
| Pérdida de energía / Energía inicial | 0.29 | 0.296 |
En vista de estos resultados, podríamos esperar una cantidad considerable de tiempo de cómputo para lograr tal precisión. De hecho, el tiempo total de la CPU en un ordenador de escritorio Pentium 4, 3.20GHz fue de solo 88 segundos. Un tiempo de computación tan corto requiere una explicación y ese es el propósito de las siguientes secciones.
..
¿Por qué la técnica VOF funciona bien?
Hay algunos conceptos generales sobre los métodos computacionales y la técnica VOF en particular que pueden usarse para comprender cómo y por qué VOF funciona de manera tan eficiente.
Teoría Básica
Todos los métodos numéricos deben usar alguna simplificación para reducir un problema de fluido a un conjunto finito de valores numéricos que luego pueden manipularse mediante operaciones aritméticas elementales. Un procedimiento típico para aproximar un fluido continuo mediante un conjunto discreto de valores numéricos es subdividir el espacio ocupado por el fluido en una malla que consiste en un conjunto de “bloques” pequeños, a menudo rectangulares. Dentro de cada elemento se aplica un proceso de promediado para obtener valores representativos del elemento para la presión, densidad, velocidad y temperatura del fluido.
Las ecuaciones simples pueden utilizarse para realizar una aproximación de cómo los valores de cada elemento interactúan con los elementos de alrededor a lo largo del tiempo. Por ejemplo, la densidad de un elemento solo puede cambiar cuando hay un flujo neto de masa intercambiada entre un elemento y sus vecinos (es decir, conservación de masa). La velocidad del material que transporta la masa entre elementos se calcula a partir de la conservación del impulso, generalmente expresada en forma de ecuaciones de Navier-Stokes, que utiliza las presiones y las tensiones viscosas que actúan entre los elementos vecinos para aproximarse a las velocidades cambiantes del fluido en los elementos.
La idea de un elemento interactuando con sus vecinos es esencialmente lo que se entiende por una ecuación diferencial parcial, es decir, evaluar los efectos de pequeños cambios causados por la variación en cantidades cercanas.
Las ecuaciones diferenciales parciales normalmente se definen en libros de texto de ingeniería como el límite de aproximaciones hechas con volúmenes de control pequeños cuyos tamaños se reducen a valores infinitesimales. En una simulación numérica, se hace lo mismo, excepto que los tamaños de volumen de control no se pueden llevar al límite porque eso requeriría demasiados elementos de los que realizar un seguimiento. En la práctica, el objetivo es utilizar elementos suficientes para resolver los fenómenos de interés en un mínimo tiempo.
Las operaciones aritméticas asociadas con un elemento generalmente involucran solo suma, resta, multiplicación y división. Mientras que una simulación requiere que estas operaciones se realicen para miles o incluso millones de elementos, y que se repitan durante muchos intervalos de tiempo pequeños. Los ordenadores son ideales para realizar este tipo de operaciones repetitivas muy rápidamente.
La simulación del movimiento de un fluido con superficie libre introduce la complejidad de tener que lidiar con regiones de la solución cuyas formas cambian con el tiempo. Una manera conveniente de lidiar con esto es usar la técnica de Volumen de Fluido (VOF) que se describe a continuación.
.
El concepto VOF
La técnica VOF se basa en la idea de registrar en cada celda de la malla la parte fraccionaria del volumen de la celda que está ocupada por el líquido. Normalmente, el volumen fraccional se representa por la cantidad F. Como es un volumen fraccionario, F debe tener un valor entre 0.0 y 1.0.
En regiones interiores de líquido, el valor de F sería 1.0, mientras que fuera del líquido, en regiones de gas (aire, por ejemplo), el valor de F es cero. La ubicación de una superficie libre es donde F cambia de 0.0 a 1.0. Por lo tanto, cualquier elemento que tenga un valor de F entre 0.0 y 1.0 debe contener una superficie libre.
Es importante enfatizar que la técnica VOF no define directamente una superficie libre, sino que define la ubicación de un volumen de fluido. Es por esta razón que las regiones de fluido pueden unirse o romperse sin causar dificultades de cálculo. Las superficies libres son simplemente una consecuencia de donde la fracción de volumen de fluido pasa de 1.0 a 0.0. Esta es una característica muy deseable que hace que la técnica VOF sea aplicable a casi cualquier tipo de problema de superficie libre.
Otra característica importante de la técnica VOF es que registra la ubicación del fluido asignando un solo valor numérico (F) a cada elemento de la malla. Esto es completamente consistente con el monitoreo de todas las demás propiedades del fluido en un elemento como la presión y las componentes de la velocidad por sus valores promedio.
.
Algunos detalles de la técnica VOF
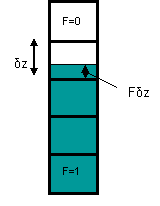
Para propósitos de precisión, es deseable tener una forma de ubicar una superficie libre dentro de un elemento. Teniendo en cuenta los valores de F en los elementos vecinos, se puede hacer esto fácilmente. Por ejemplo, imagine una columna unidimensional de elementos en la que una parte de la columna está llena de líquido, Fig. 3. La superficie del líquido está en un elemento en la región central de la columna, que se denominará elemento de superficie. Debido a que asumimos que los valores de F deben ser 0.0 o 1.0, excepto en el elemento de superficie, podemos usar esto para ubicar la posición exacta de la superficie. Primero se hace una prueba para ver si la superficie se encuentra en la parte superior o inferior. Si el elemento sobre el elemento de superficie está vacío de líquido, la superficie debe ser una superficie superior. En caso contrario es una superficie inferior.
Para una superficie superior, calculamos su ubicación exacta situada sobre el borde inferior del elemento de superficie por una distancia igual a F por el tamaño vertical del elemento. Una superficie inferior se ubica de manera similar a una distancia igual a F por el tamaño vertical del elemento debajo del borde superior del elemento superficial. La ubicación de la superficie dentro de un elemento de esta manera se desprende de la definición de F como un volumen fraccionario de líquido en el elemento.
El cálculo de las ubicaciones de la superficie en columnas unidimensionales es simple, preciso y requiere muy poca aritmética. Sin embargo, en situaciones bidimensionales y tridimensionales, calcular una ubicación es un poco más complicado porque existe un rango continuo de orientaciones de superficie posibles dentro de una celda de superficie. Sin embargo, lidiar con esto no es difícil. Un ejemplo bidimensional, la Fig. 4, ilustrará una manera simple no solo de calcular la ubicación de la superficie, sino también de obtener una buena idea de su pendiente y curvatura.
Como en el caso unidimensional, primero es necesario encontrar la orientación aproximada de la superficie probando los elementos vecinos. En la Fig. 4, la dirección normal exterior sería la más cercana a la dirección ascendente porque la diferencia en los valores vecinos en esa dirección es mayor que en cualquier otra dirección.
A continuación, las alturas locales de la superficie se calculan en columnas de elementos que se encuentran en la dirección normal aproximada. Para el caso bidimensional en la Fig. 4, estas alturas se indican mediante flechas. Finalmente, la altura en la columna que contiene el elemento de superficie proporciona la ubicación de la superficie en ese elemento, mientras que las otras dos alturas se pueden usar para calcular la pendiente de la superficie local y la curvatura de la superficie.
En tres dimensiones se usa el mismo procedimiento, aunque las alturas de las columnas deben evaluarse para nueve columnas alrededor del elemento de superficie. Aunque se necesita un poco más de cálculo, consiste principalmente en sumas simples en las columnas y luego sumas y diferencias de alturas de columnas para evaluar la pendiente y la curvatura.
Hay dos asuntos pendientes para tratar. Un problema es que una simulación como esa en las Figs. 1 y 2 solo resuelve la dinámica de fluidos en regiones donde hay fluidos. Esta es otra razón para la eficiencia computacional del método VOF. La región ocupada por el fluido en el flujo en un problema con escalón es mucho menos que la mitad de la región abierta en la malla computacional. Si fuera necesario resolver también el flujo de gas que rodea el líquido, se requeriría un tiempo de computación considerablemente mayor. Sin embargo, para calcular soluciones solo en el líquido, es necesario especificar condiciones de contorno sobre la superficie libre. Estas condiciones son la desaparición de la tensión tangencial y la aplicación de una presión normal en la superficie que es igual a la presión del gas.
Un segundo problema es que el movimiento y la deformación de la superficie libre se debe calcular resolviendo la fracción de fluido, F, a medida que se mueve con el fluido. Debido a que la variable F es discontinua (es decir, principalmente 0.0 o 1.0), se debe tener cuidado para mantener esta discontinuidad a medida que se mueve a través de la malla computacional. En el método VOF, se utilizan algoritmos de advección especiales para este propósito.
.
Ilustración del seguimiento de superficie libre por la técnica VOF
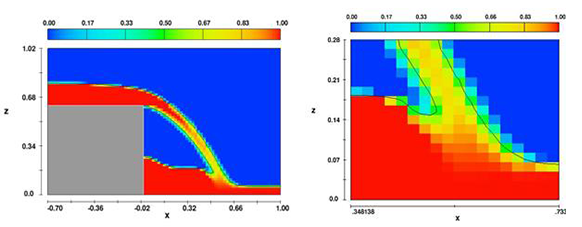
La Figura 6a es una ilustración de qué tan bien funciona esto; la fracción de volumen del fluido está coloreada uniformemente en cada elemento de la malla para representar su valor en ese elemento. La superficie libre se define claramente en todas partes. Solo en la parte más baja y más estrecha de la vena hay una pérdida notable de la distribución adecuada de la fracción fluida, Fig. 5b. Esto se esperaba porque en esta región de la vena, se tienen menos de tres elementos en su espesor y esto permite que algunos de los valores F más pequeños asociados con elementos de superficie parcialmente llenos se mezclen con el elemento central, que debería tener un valor de 1.0. Para fines computacionales, esto no importa realmente porque el método de simulación trata los elementos internos del líquido como si fueran elementos líquidos puros.
También debe señalarse que en la región que se muestra en la Fig. 5b, la turbulencia y la entrada de aire se observan en experimentos reales. Por lo tanto, la aparición de valores de fracción de fluidos un poco menos que la unidad es algo realista. Esto no es totalmente accidental debido a que la intersección del chorro de líquido con una piscina, que es responsable de la turbulencia y la entrada de aire, también es responsable del «arrastre» de valores de fracción de fluido en el interior del líquido.
Resumen
Al principio, puede parecer algo mágico que un ordenador pueda realizar operaciones aritméticas repetidas en matrices de números y producir una simulación realista de un problema complejo, dependiente del tiempo, de dinámica de fluidos.
Utilizando un ejemplo de flujo hidráulico simple, pero no trivial, se ha demostrado que las simulaciones computacionales pueden producir resultados detallados en concordancia con las mediciones físicas. Además, se ha demostrado que la simulación, que se basó en la técnica de Volumen de Fluido (VOF), utiliza métodos de aproximación simples que son precisos y eficientes.
Claramente, los ejemplos del mundo real que involucran estructuras hidráulicas complejas, como las que se usan en las centrales hidroeléctricas, deben consumir más que los pocos segundos de tiempo de computación utilizados en nuestro ejemplo para obtener resultados útiles. Sin embargo, esos resultados se pueden generar en tiempos razonables (tanto para el hombre como para el ordenador) y contiene una amplitud de detalles que rara vez es posible en experimentos físicos.
.
Postscript
La primera descripción detallada del método VOF fue en 1981 por C.WHirt y B.D.Nihols, J. Comp. Phys., 39, p.201. Todas las simulaciones que aparecen en este artículo se desarrollan con el software CFD comercial FLOW-3D desarrollado por Flow Science, Inc. Este software CFD emplea una variación mejorada del método VOF denominado TruVOF.